Interactive
GPU Programming
with ClojureCUDA
and ClojureCL

Dragan Djuric

[email protected]

Dragan Djuric

Clojure and FP are great!

  • Dynamic and fast
  • First-class functions
  • Great abstractions and data structures
  • Many useful libraries
  • Even more experimental libraries
  • Access to Java and the JVM
  • Hey, the community is amazing!

What I'll talk about?

  • Not (necessarily) Big Data
  • Lots of computations regardless of data size
  • numerical data
  • numerical algorithms

Is FP good at number crunching?

  • Good? sometimes.
  • Great? NO!
  • Poor access to hardware-specific optimizations.
  • Some FP ideas are very useful!

CPU is not so great either!

  • R, Python? Even worse than Java or Hasekell.
  • C? complicated, verbose platform-specific optimizations.
  • CPU? too beefed-up!

GPU has a lot to offer …at a price

  • many dumb computing units
  • but, power-efficient for number crunching
  • hardware support for massive parallelism
  • faster and cheaper each year
  • notoriously difficult to program

Uncomplicate

ClojureCL
take control of the GPU, CPU, and accelerators from Clojure
ClojureCUDA
take control of the Nvidia GPU
Neanderthal
vectors and matrices, but optimized for CPU and GPU
Bayadera
high performance Bayesian statistics and data analysis on the GPU

Hello world: dot product

  • One of the simplest linear algebra functions
  • Consists of two familiar FP building blocks:
    • map
    • reduce
  • Multiply each corresponding element of two arrays (vectors) and add them up.

Idiomatic Clojure

(let [dot-product (fn [xs ys]
                    (reduce + (map * xs ys)))

      x-vec (vec (range 100000))
      y-vec (vec (range 100000))]

  (dot-product x-vec y-vec))

333328333350000

Execution time: 14 ms

Neanderthal: using optimized library

(let [x (fv (range 100000))
      y (copy x)]

  (dot x y))

3.33328352E14
  • Execution time: 6 μs

Neanderthal: a taste of GPU

(with-default
  (with-default-engine
    (with-release [gpu-x (cuv (range 100000))
                   gpu-y (copy gpu-x)]

      (dot gpu-x gpu-y))))

3.33328352E14
  • Execution time: 26 μs
  • Not faster than the CPU at all! Why?

A million dot products on the GPU

(with-default
  (with-default-engine
    (with-release [gpu-x (entry! (cuge 1000 100000) 0.01)
                   gpu-y (copy (trans gpu-x))
                   cpu-c (cuge 1000 1000)]

      (do (mm! 1 gpu-x gpu-y 0 cpu-c)
          (synchronize!)
          true))))

true
  • Execution time: 23 ms
  • 23 nanoseconds per a 100000 element dot product!
  • Our Clojure code started from 14 milliseconds (600,000 × difference!)
  • 1000 × faster than a solo dot product!

A glimpse of ClojureCUDA API

(init)

true

(device-count)

2

(def my-nvidia-gpu (device 0))

#'user/my-nvidia-gpu

Querying information

(info my-nvidia-gpu)

{:max-grid-dim-y 65535, :total-mem 11721506816,
 :name "GeForce GTX 1080 Ti", :max-threads-per-multiprocessor 2048,
 :max-shared-memory-per-block 49152, :compute-capability-major 6,
 :global-memory-bus-width 352, :memory-clock-rate 5505000,
 :max-threads-per-block 1024, :multiprocessor-count 28,
 :warp-size 32, :max-registers-per-block 65536
 ;;... much more data
}

Managing Context

(def ctx (context my-nvidia-gpu))

#'user/ctx

(info ctx)

{:dev-runtime-pending-launch-count 2048  :dev-runtime-sync-depth 2
 :malloc-heap-size 8388608  :stack-size 1024  :api-version 3020
 :stream-priority-range (0 -1)  :cache-config :prefer-none  :printf-fifo-size 1048576
 :device #object(jcuda.driver.CUdevice 0x12be4426 "CUdevice[nativePointer=0x0]")
 :shared-config :four-byte-bank-size}

(= ctx (current-context))

true

Memory

(def gpu-array (mem-alloc 1024))

#'user/gpu-array

(def main-array (float-array (range 256)))

#'user/main-array

(take 10 main-array)

(0 1 2 3 4 5 6 7 8 9)

Transfer data to GPU memory

(memcpy-host! main-array gpu-array)

#object[uncomplicate.clojurecuda.internal.impl.CULinearMemory 0x38701ca4 "uncomplicate.clojurecuda.internal.impl.CULinearMemory@38701ca4"]

(take 12 (memcpy-host! gpu-array (float-array 256)))

(0 1 2 3 4 5 6 7 8 9 10 11)

Compute something already!

The kernel

extern "C"
__global__ void increment(int n, float *a) {
    int i = blockIdx.x * blockDim.x + threadIdx.x;
    if (i < n) {
        a[i] = a[i] + 1.0f;
    }
};

The program

(def kernel-source
      "extern \"C\"
         __global__ void increment (int n, float *a) {
           int i = blockIdx.x * blockDim.x + threadIdx.x;
           if (i < n) {
             a[i] = a[i] + 1.0f;
        }
       };")

(def hello-program (compile! (program kernel-source)))

#'user/kernel-source#'user/hello-program

The GPU Function

(def hello-module (module hello-program))
(def increment (function hello-module "increment"))

#'user/hello-module#'user/increment

Running the GPU function

(launch! increment (grid-1d 256) (parameters 256 gpu-array))

nil

(take 12 (memcpy-host! gpu-array (float-array 256)))

(1 2 3 4 5 6 7 8 9 10 11 12)

Bayadera
Bayesian Data Analysis on the GPU

How to know something we cannot observe?

  • Probabilities of all answers (prior \(Pr(H)\))
  • Probability of measured data (evidence \(\Pr(D)\) and likelihood \(\Pr(D|H)\))
  • Calculate "backwards", using Bayes' rule and get
  • posterior probabilities of answers \(\Pr(H|D)\)

\(\Pr(H|D) = \frac{\Pr(D|H)\times \Pr(H)}{\Pr(D)}\)

What does all this has to do with Bayes?

  • BDA is conceptually simple
  • Real models must be calculated numerically
  • MCMC sampling and related methods
  • In higher dimensions, requires huge samples
  • Analyses typically run in minutes, hours, weeks

.

  • Good: Clojure and GPU FTW
  • Challenge: MCMC is sequential

Doing Bayesian Data Analysis

  • John Kruschke
  • Excellent tutorial, even for beginners
  • Real-world examples through the book!

dbda-book.png

Real World
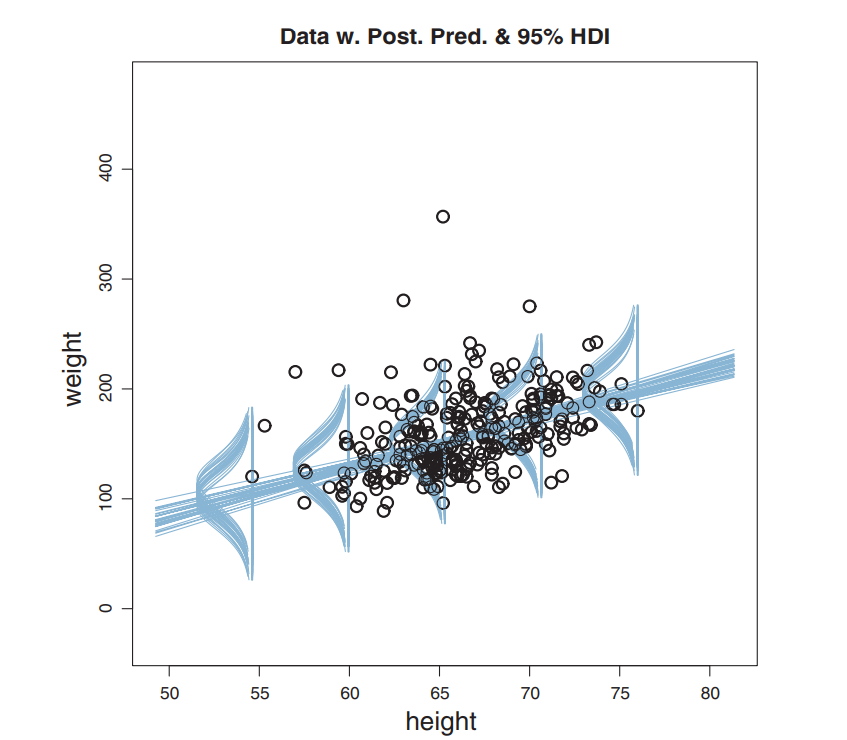
Robust Linear Regression

kruschke-hlr-data.png

Hierarchical Model

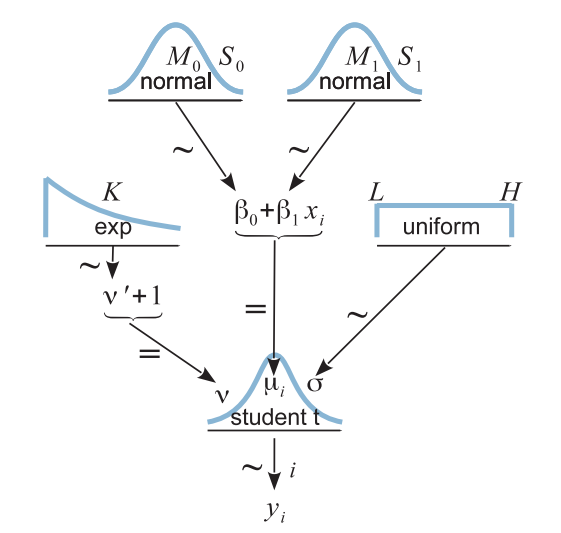
kruschke-hlr-model.png

Resulting Posterior

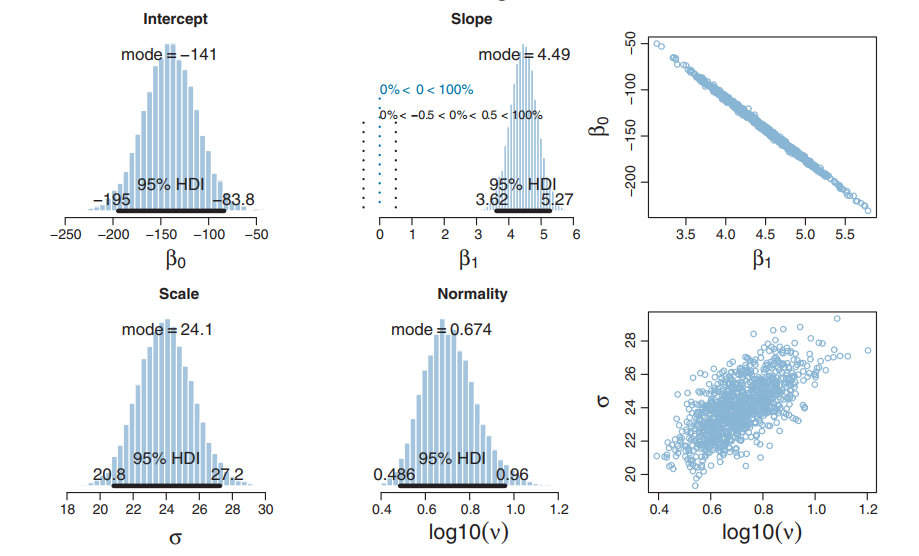
kruschke-hlr-posterior.png

Create a custom model in Bayadera

(def rlr-source (slurp (io/file "robust-linear-regression.cl")))

(defn my-prior-model-distribution []
  (library/distribution-model
   [:gaussian :uniform :exponential :student-t rlr-source]
   {:name "rlr" :mcmc-logpdf "rlr_mcmc_logpdf"
    :params-size 7 :dimension 4}))

#'user/rlr-source#'user/rlr-prior#'user/rlr-likelihood

Model's prior function

REAL rlr_logpdf(const uint data_len,
                const uint hyperparams_len,
                const REAL* params,
                const uint dim, REAL* x) {
    return exponential_log(params[0], x[0] - 1)
        + gaussian_log(params[1], params[2], x[1])
        + gaussian_log(params[3], params[4], x[2])
        + uniform_log(params[5], params[6], x[3]);
}

Model's likelihood function

REAL rlr_loglik(const uint data_len, const REAL* data,
                const uint dim, const REAL* x) {
    const REAL nu = x[0];
    const REAL b0 = x[1];
    const REAL b1 = x[2];
    const REAL sigma = x[3];
    const uint n = (uint)data[0];
    const bool valid = (0.0f < nu) && (0.0f < sigma);
    if (valid) {
        const REAL scale = student_t_log_scale(nu, sigma);
        REAL res = 0.0;
        for (uint i = 0; i < n; i = i+2) {
            res += student_t_log_unscaled(nu, b0 + b1 * data[i+1],
                                          sigma, data[i+2])
                + scale;
        }
        return res;
    }
    return NAN;
}

Running the inference on the GPU

(def result
  (with-default-bayadera
    (with-release
      [rlr-likelihood (library/likelihood-model rlr-source {:name "rlr"})
       rlr-prior (my-prior-model-distribution)
       prior (distribution rlr-prior)
       prior-dist (prior (fv 10 -100 100 5 10 0.001 1000))
       post (distribution "rlr" rlr-likelihood prior-dist)
       post-dist (post params-300)
       post-sampler(sampler post-dist
                            {:limits (fge 2 4 [1 10 -400 100 0 20 0.01 100])})]
      (mix! post-sampler {:step 384})
      (histogram! post-sampler 1000))))

Fine grained histograms!

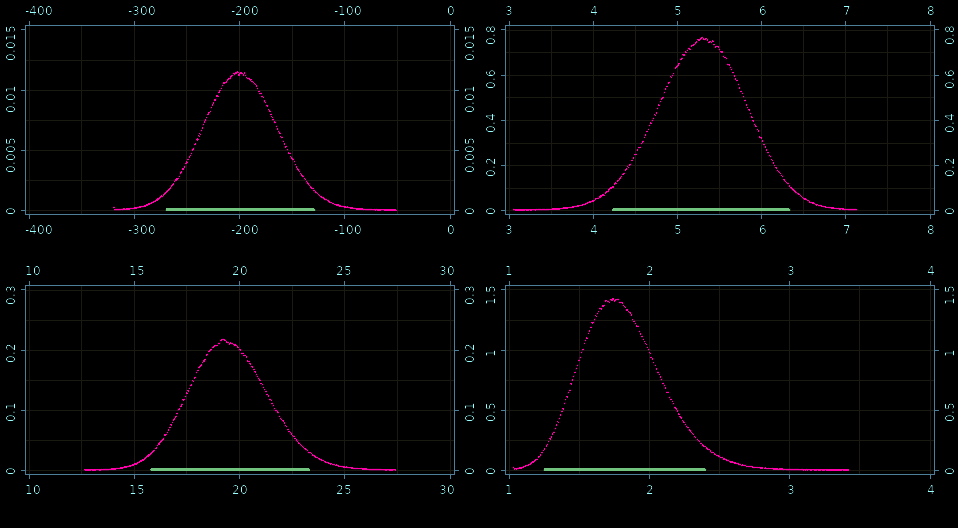
Posteriors: β0, β1,σ, and ν robust-linear-regression.png

How fast is it?

  • Bayadera
    • 61,208,576 samples in 267 ms.
    • 4.36 ns per (computationally heavy) sample
    • very precise histogram
  • JAGS/Stan (state-of-the-art bayesian C++ tools)
    • 20,000 samples in 180/485 seconds
    • 9 ms per sample
    • rough histogram
  • 2,000,000 × faster per sample
  • more precise results, 1000 × faster

In real life

  • 1 second vs a couple of hours
  • 1 minute vs several days!
  • 1 hour vs couple months/ a year

Adopt a pet function

Thank you for donations
https://patreon.com/draganrocks