Deep Learning from Scratch to GPU - 4 - Increasing Performance with Batch Processing
February 18, 2019
Please share this post in your communities. Without your help, it will stay burried under tons of corporate-pushed, AI and blog farm generated slop, and very few people will know that this exists.
These books fund my work! Please check them out.
If you haven't yet, read my introduction to this series in Deep Learning in Clojure from Scratch to GPU - Part 0 - Why Bother?.
The previous article, Part 3, is here: Fully Connected Inference Layers.
To run the code, you need a Clojure project with Neanderthal () included as a dependency. If you're in a hurry, you can clone Neanderthal Hello World project.
Don't forget to read at least some introduction from Neural Networks and Deep Learning, start up the REPL from your favorite Clojure development environment, and let's continue with the tutorial.
(require '[uncomplicate.commons.core :refer [with-release let-release Releaseable release]] '[uncomplicate.neanderthal [core :refer [mv! axpy! scal! transfer! col mm! mm rk! entry! copy!]] [native :refer [dv dge]] [vect-math :refer [tanh! linear-frac!]]] '[criterium.core :refer [quick-bench]]) (import 'clojure.lang.IFn)
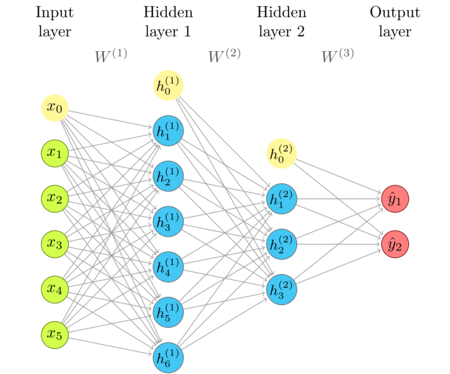
The network diagram
I'm repeating the network diagram from the previous article as a convenient reference.
The idea of batch processing
The current processing of the network, shown above, is such that
each input vector is threaded through layers, transformed by a series of matrices and
non-linear activation functions, to produce an output vector. The heart of the implementation
is the matrix-vector product operation (mv!), which is performed by optimized high performance libraries
(Neanderthal in this case).
If we have only one input instance to process, there is not much that we can do to speed that up. However, we often have many input instances that we would like to process, either at once, or in a short period. Instead of calling the network function for each of these instances in a loop, we can process the whole batch using matrix functions that do the equivalent thing, but in an optimized way. We will process the whole batch at once.
Consider a matrix \(A\) and its columns. If we want to transform all these columns by
a matrix transformation \(T\), we can do this by invoking a matrix-vector product (mv!) for each column of \(A\).
As I discussed in matrix transformations, we can get the same result
by doing a matrix-matrix multiplication of \(T\) and \(A\). Matrix-matrix multiplication
has more space for hardware optimization than looping over simpler matrix-vector multiplications,
and it will be faster.
Let's see the difference!
(def t (dge 1000 1000)) (def a (dge 1000 10000)) (def y (dv 1000)) (def b (dge 1000 10000))
(time (dotimes [i 10000] (mv! t (col a i) y)))
"Elapsed time: 987.553046 msecs"
(time (mm! t a b))
"Elapsed time: 102.086963 msecs"
For this particular size of input (1000) and batch (10000), on my CPU (i7-4790k), matrix-matrix multiplication is roughly 10 times faster than the equivalent loop of 10000 matrix-vector multiplications.
The exact difference in performance depends on the hardware and the matrix dimensions. The rule of thumb is that the speed-up is higher for larger matrices. In consequence, since the input dimension of a network stays constant, we expect that the network speed per input vector increases with larger batch size.
On the GPU, the difference is even more noticeable than on the CPU. We will explore this soon, when we support GPU computing.
Batched layer processing
(def x (dge 2 1 [0.3 0.9])) (def w1 (dge 4 2 [0.3 0.6 0.1 2.0 0.9 3.7 0.0 1.0] {:layout :row})) (mm w1 x)
nil#'user/x#'user/w1#RealGEMatrix[double, mxn:4x1, layout:column, offset:0] ▥ ↓ ┓ → 0.63 → 1.83 → 3.60 → 0.90 ┗ ┛
As we can see, transforming an \(m\times{1}\) matrix is equivalent to transforming its only column.
(defn sigmoid! [x] (linear-frac! 0.5 (tanh! (scal! 0.5 x)) 0.5))
We have a problem of how to handle bias, though. Bias is a vector.
(def bias-vector (dv 0.7 0.2 1.1 2))
Calling axpy! to add a bias vector to the \(Wx\) matrix, will throw an exception.
(sigmoid! (axpy! -1.0 bias-vector (mm w1 x)))
nilclass java.lang.ClassCastExceptionclass java.lang.ClassCastExceptionExecution error (ClassCastException) at uncomplicate.neanderthal.internal.host.mkl.DoubleVectorEngine/axpy (mkl.clj:413). uncomplicate.neanderthal.internal.host.buffer_block.RealGEMatrix cannot be cast to uncomplicate.neanderthal.internal.host.buffer_block.RealBlockVector
We could temporarily solve this issue in the same way as turning the input vector to a \(m\times{1}\) matrix.
(def bias-matrix (dge 4 1 [0.7 0.2 1.1 2]))
(sigmoid! (axpy! -1.0 bias-matrix (mm w1 x)))
nil#RealGEMatrix[double, mxn:4x1, layout:column, offset:0] ▥ ↓ ┓ → 0.48 → 0.84 → 0.92 → 0.25 ┗ ┛
The result is the same as in part 2, Bias and Activation Function. However, this does not work with batch sizes larger than 1, since the bias is the same for all inputs. We could turn it into a matrix where we repeat the same bias column as many times as we need. This would almost double the memory required to hold the network. We can't accept such waste!
Vector broadcasting
We need a way to broadcast that vector to all columns of the matrix. I've already written an article that discussed a few ways of implementing this, including performance considerations.
One convenient solution is to use the rk! function, which cross-multiplies
two vectors, adding the product matrix to the resulting matrix of the matching dimensions.
(let-release [a (dge 3 2 (repeat 6 1000))] (with-release [x (dv 1 2 3) y (dv 20 30)] (rk! 2 x y a)))
nil#RealGEMatrix[double, mxn:3x2, layout:column, offset:0] ▥ ↓ ↓ ┓ → 1040.00 1060.00 → 1080.00 1120.00 → 1120.00 1180.00 ┗ ┛
In this case, the entry in the first row of the second column is \(2 \times 1 \times 30 + 1000 = 1060\).
We can use rk! to implement vector broadcast by cross-multiplying the vector of ones by the vector
that we want to broadcast and adding it to the matrix that we want the vector broadcast to.
(let-release [a (dge 3 2 (repeat 6 1000))] (with-release [x (dv 1 2 3) ones (entry! (dv 2) 1)] (rk! x ones a)))
nil#RealGEMatrix[double, mxn:3x2, layout:column, offset:0] ▥ ↓ ↓ ┓ → 1001.00 1001.00 → 1002.00 1002.00 → 1003.00 1003.00 ┗ ┛
In this example, the vector x has been added to each column of the matrix a.
Batched layer implementation
We will redefine the FullyConnectedinference type, to support both single and batched input and output.
(defprotocol Parameters (weights [this]) (bias [this])) (deftype FullyConnectedInference [w b h activ-fn] Releaseable (release [_] (release w) (release b) (release h)) Parameters (weights [this] w) (bias [this] b) IFn (invoke [_ x] (activ-fn (axpy! -1.0 b (mv! w x h)))) (invoke [_ x ones a] (activ-fn (rk! -1.0 b ones (mm! 1.0 w x 0.0 a)))))
We use mm! (matrix-matrix multiplication) instead of mv! (matrix-vector multiplication).
Since we'd like to support arbitrary batch sizes, we provide the input matrix x, the broadcast helper ones,
and the output matrix a as the arguments of the invoke function. If we kept a and ones as fields,
in the same way as h, the size of the batch would be fixed to their dimensions.
To support both vectors and matrices in the activation function, I separated the bias subtraction from the activation function and moved it to the invoke method itself.
Note how the only change is that instead of a simple addition of matching structures (axpy!), we are
using the rk! powered vector-matrix broadcast.
This is an effective solution. Unfortunately, the same simple change can not be applied
to our implementation of the relu activation function. We will skip relu at the moment, and find
the best way to support it later.
The constructor, fully-connected does not require any changes.
(defn fully-connected [activ-fn in-dim out-dim] (let-release [w (dge out-dim in-dim) bias (dv out-dim) h (dv out-dim)] (->FullyConnectedInference w bias h activ-fn)))
Using already existing x, bias-matrix and w1, we get the same result as before.
(let-release [a (dge 4 1)] (with-release [layer-1 (fully-connected sigmoid! 2 4) ones (dv [1])] (copy! w1 (weights layer-1)) (copy! bias-vector (bias layer-1)) (layer-1 x ones a)))
nil#RealGEMatrix[double, mxn:4x1, layout:column, offset:0] ▥ ↓ ┓ → 0.48 → 0.84 → 0.92 → 0.25 ┗ ┛
The result is as expected.
Micro benchmark
Let's compare the performance of the batched implementation with the results we have got in Part 3.
(with-release [x (dge 10000 10000) ones (entry! (dv 10000) 1) layer-1 (fully-connected tanh! 10000 5000) a1 (dge 5000 10000) layer-2 (fully-connected sigmoid! 5000 1000) a2 (dge 1000 10000) layer-3 (fully-connected sigmoid! 1000 10) a3 (dge 10 10000)] (time (-> x (layer-1 ones a1) (layer-2 ones a2) (layer-3 ones a3))))
On the same machine that required 18 ms per one input column, my 5 year old CPU (i7-4790k), I get 6 seconds for the batched version.
"Elapsed time: 6012.853561 msecs"
Compared to 18 ms × 10000, which gives 180 seconds, the batched implementation, at 6 seconds, is roughly 30 times faster! The difference in performance is typically positively correlated to the batch and input size.
This is a significant gain, since the logic stays the same and the required changes are minimal. The important lesson is that we should prefer vectored operations instead of writing manual loops whenever possible.
The next article
Step by step, we explored the basic building blocks of fully connected inference layers.
The version with batched inference introduced a complication with supplying a vector of ones, and the need to supply large matrices to hold outputs of each layer.
There is just one thing that we need to discuss before we generalize the inference layer and run it on the GPU!
After that, we are ready to tackle the implementation of learning. It may seem to you that I'm obsessing about implementation details too much, but you'll see that we will use them to great benefit once we tackle the harder challenge. Then, you will not hit a wall, because you'd already be prepared and have them in your toolbox.
On Thursday (or right away, if you're not reading this right away), read about Reusing Memory!
Thank you
Clojurists Together financially supported writing this series. Big thanks to all Clojurians who contribute, and thank you for reading and discussing this series.

