Deep Learning from Scratch to GPU - 11 - A Simple Neural Network Inference API

Need help with your custom Clojure software? I'm open to (selected) contract work.

March 28, 2019

Please share: Twitter.

These books fund my work! Please check them out.

The time is ripe for wrapping what we have built so far in a nice Neural Network API. After all, who would want to assemble networks by hand?

If you haven't yet, read my introduction to this series in Deep Learning in Clojure from Scratch to GPU - Part 0 - Why Bother?.

The previous article, Part 10, is here: The Backward Pass.

To run the code, you need a Clojure project with Neanderthal () included as a dependency. If you're in a hurry, you can clone Neanderthal Hello World project.

Don't forget to read at least some introduction from Neural Networks and Deep Learning, start up the REPL from your favorite Clojure development environment, and let's continue with the tutorial.

The network diagram

I'm repeating the network diagram from the previous article as a convenient reference.

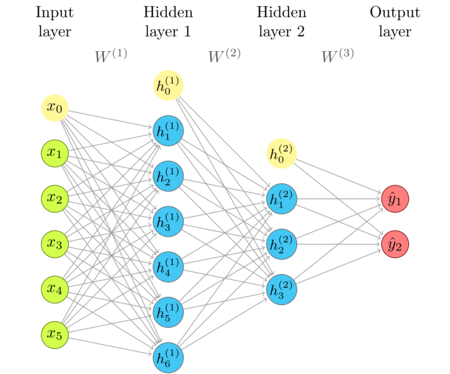
Defining a simple NN API

Taking a look at the diagram, we conclude that we need the following information to define a neural network on a high level:

1) the kind of each layer (default available)
2) the number of neurons in each layer
3) connections between layers (default available)
4) the activation at each layer (default available)
5) the cost function and its derivative at the output (default available)

In this tutorial, we are supporting sequential layers. It is possible to connect layers in a complicated network, but a traditional approach will be able to achieve a lot with just a linear sequence of layers. Fully connected and convolutional layers are the most popular layer kinds. We have implemented fully connected layers and will use this as the default choice. From a handful of activation functions that are most commonly used, we will choose sigmoid as the default. The cost function is relevant only at the output, and let the default be the mean squared error for the time being.

Functional API

Here's a draft of how using a NN API could look like, based on how we used the functions we have created by now.

(def input (fv 1000))
(def output (fv 8))
(def inference (net factory
                    [(fully-connected sigmoid 1000 256)
                     (fully-connected tanh 256 64)
                     (fully-connected sigmoid 64 16)]))
(def train (training inference input output quadratic-cost))
(sgd train 20)

The advantage of the first option is that it gives users the absolute freedom of choice to work with, test, and combine each building block on its own. It exposes the integration points for new implementations of layers, activations, the way they are invoked, or the way they share resources. This would cater to a user most interested in the software engineering side of deep learning. It may not be so attractive to users whose primary task is to analyze data, since it taxes them with details, while the default implementation is good in most cases.

Declarative descriptors

Another approach is to define a DSL for creating a declarative specification of the network, and an engine for translating such descriptors into an executable form.

(def network-desc (network {:input 1000
                            :layers [{:type :fc :activation :sigmoid :size 256}
                                     {:type :fc :activation :tanh :size 64}
                                     {:type :fc :activation :sigmoid :size 16}]}))
(def infer (inference factory network-desc))
(def train (training inference input output quadratic-cost))
(sgd train)

This approach may seem to be the most pleasant at first: just describe what you want, and let the engine configure the implementation for you. The advantage is that you can write whatever you like in a flexible form. However, if there is an error in your declaration, good luck finding what the problem might be. If you want to add or change an implementation detail, also good luck :)

Functional API with declarative options

In this series, I'll choose, in my opinion, a good middle ground. I choose to offer control over individual peaces and extensible hooks, while filling in sensible details, and use declarative options in places where that makes sense.

...
(def input (fv 1000))
(def output (fv 8))
(def inference (net factory 1000
                    [(fully-connected 256 sigmoid)
                     (fully-connected 64 tanh)
                     (fully-connected 16 sigmoid)]))
(def train (training inference input output quadratic-cost))
(sgd train 20)
...

Treat these sketches as illustrations, though, not as complete specifications. We'll discover what works step by step.

The result, I hope, will be something that is rather nice to use (for programmers at least). Unfortunately, once we wish to support integration with deep neural networks performance libraries such as cuDNN or MKL-DNN, we will have to complicate this a bit, since these libraries mandate tensor descriptor-based approach which is more static and highly involved. There's a nice education value in writing something nicer and simpler, yet fully functional, at first, so we will go our way!

I hope I won't give out a spoiler if I tell you that our fully connected implementation might turn out to be faster than the one assembled from corresponding MKL-DNN primitives.

The existing pieces

First, the imports and requires that we will need.

(require '[uncomplicate.commons.core
           :refer [with-release let-release Releaseable release]]
         '[uncomplicate.clojurecuda.core :as cuda
           :refer [current-context default-stream synchronize!]]
         '[uncomplicate.clojurecl.core :as opencl
           :refer [*context* *command-queue* finish!]]
         '[uncomplicate.neanderthal
           [core :refer [mrows ncols dim raw view view-ge vctr copy row
                         entry! axpy! copy! scal! mv! transfer! transfer
                         mm! rk! view-ge vctr ge trans nrm2]]
           [math :refer [sqr]]
           [vect-math :refer [tanh! linear-frac! sqr! mul! cosh! inv!]]
           [native :refer [fge native-float]]
           [cuda :refer [cuda-float]]
           [opencl :refer [opencl-float]]])
(import 'clojure.lang.IFn)

Here is the code that we developed in the last article.

(defprotocol Parameters
  (weights [this])
  (bias [this]))

(defprotocol ActivationProvider
  (activation-fn [this]))

(deftype FullyConnectedInference [w b activ-fn]
  Releaseable
  (release [_]
    (release w)
    (release b)
    (release activ-fn))
  Parameters
  (weights [_] w)
  (bias [_] b)
  ActivationProvider
  (activation-fn [_] (activ-fn))
  IFn
  (invoke [_ x ones a]
    (activ-fn (rk! -1.0 b ones (mm! 1.0 w x 0.0 a)))))

(defn fully-connected [factory activ-fn in-dim out-dim]
  (let-release [w (ge factory out-dim in-dim)
                bias (vctr factory out-dim)]
    (->FullyConnectedInference w bias activ-fn)))

(defprotocol Backprop
  (forward [this])
  (backward [this eta]))

(defprotocol Transfer
  (input [this])
  (output [this])
  (ones [this]))

(defprotocol Activation
  (activ [_ z a!])
  (prime [_ z!]))

(deftype FullyConnectedTraining [v w b a-1 z a ones activ-fn]
  Releaseable
  (release [_]
    (release v)
    (release w)
    (release b)
    (release a-1)
    (release z)
    (release a)
    (release ones)
    (release activ-fn))
  Parameters
  (weights [_] w)
  (bias [_] b)
  Transfer
  (input [_] a-1)
  (output [_] a)
  (ones [_] ones)
  Backprop
  (forward [_]
    (activ activ-fn (rk! -1.0 b ones (mm! 1.0 w a-1 0.0 z)) a))
  (backward [_ eta]
    (let [eta-avg (- (/ (double eta) (dim ones)))]
      (mul! (prime activ-fn z) a) ;; (1 and 2)
      (mm! eta-avg z (trans a-1) 0.0 v) ;; (4)
      (mm! 1.0 (trans w) z 0.0 a-1) ;; (2)
      (mv! eta-avg z ones 1.0 b) ;; (3)
      (axpy! 1.0 v w))))

(defn training-layer
  ([inference-layer input ones-vctr]
   (let-release [w (view (weights inference-layer))
                 v (raw w)
                 b (view (bias inference-layer))
                 a-1 (view input)
                 z (ge w (mrows w) (dim ones-vctr))
                 a (raw z)
                 o (view ones-vctr)]
     (->FullyConnectedTraining v w b a-1 z a o ((activation-fn inference-layer) z))))
  ([inference-layer previous-backprop]
   (training-layer inference-layer
                   (output previous-backprop)
                   (ones previous-backprop))))

(deftype SigmoidActivation [work]
  Releaseable
  (release [_]
    (release work))
  Activation
  (activ [_ z a!]
    (linear-frac! 0.5 (tanh! (scal! 0.5 (copy! z a!))) 0.5))
  (prime [this z!]
    (linear-frac! 0.5 (tanh! (scal! 0.5 z!)) 0.5)
    (mul! z! (linear-frac! -1.0 z! 1.0 work))))

(defn sigmoid
  ([]
   (fn [z]
     (let-release [work (raw z)]
       (->SigmoidActivation work))))
  ([z!]
   (linear-frac! 0.5 (tanh! (scal! 0.5 z!)) 0.5)))

(deftype TanhActivation []
  Activation
  (activ [_ z a!]
    (tanh! z a!))
  (prime [this z!]
    (sqr! (inv! (cosh! z!)))))

(defn tanh
  ([]
   (fn [_] (->TanhActivation)))
  ([z!]
   (tanh! z!)))

Checking whether the structure fits nicely:

(with-release [x (ge native-float 2 2 [0.3 0.9 0.3 0.9])
               ones (vctr native-float 1 1)
               layer-1 (fully-connected native-float tanh 2 4)
               layer-2 (fully-connected native-float sigmoid 4 1)
               training-layer-1 (training-layer layer-1 x ones)
               training-layer-2 (training-layer layer-2 training-layer-1)]
  (transfer! [0.3 0.1 0.9 0.0 0.6 2.0 3.7 1.0] (weights layer-1))
  (transfer! [0.7 0.2 1.1 2] (bias layer-1))
  (transfer! [0.75 0.15 0.22 0.33] (weights layer-2))
  (transfer! [0.3] (bias layer-2))
  (forward training-layer-1)
  (forward training-layer-2)
  (backward training-layer-2 0.05)
  (backward training-layer-1 0.05)
  (transfer (output training-layer-2)))

: nil#RealGEMatrix[float, mxn:1x2, layout:column, offset:0]
:    ▥       ↓       ↓       ┓
:    →       0.44    0.44
:    ┗                       ┛

So far, so good.

The NeuralNetworkInference deftype

Implementing inference is simpler than implementing training. Following the separation between the inference and training types, we'll start with a stand-alone NeuralNetworkInference. Looking at the usage example, I can imagine it holding a sequence of layers, and implementing the invoke method of the IFn interface.

Since a network will typically contain several layers, it would be a good thing if it reused the instances of all throw-away objects, such as the vector of ones, or an additional shared matrix for inputs and outputs. Since we want to support arbitrary batch sizes, we would have to create and release these temporary objects on each invocation.

The following invoke implementations might seem too dense at first, but they are nothing more than the automation of the code we were writing by hand until now in the test examples when we were assembling the network and calling the inference by hand.

(deftype NeuralNetworkInference [layers
                                 ^long max-width-1
                                 ^long max-width-2]
  Releaseable
  (release [_]
    (doseq [l layers] (release l)))
  IFn
  (invoke [_ x ones-vctr temp-1! temp-2!]
    (let [batch (dim ones-vctr)]
      (loop [x x v1 temp-1! v2 temp-2! layers layers]
        (if layers
          (recur (let [layer (first layers)]
                   (layer x ones-vctr
                          (view-ge v1 (mrows (weights layer)) batch)))
                 v2 v1 (next layers))
          x))))
  (invoke [this x a!]
    (let [cnt (count layers)]
      (if (= 0 cnt)
        (copy! x a!)
        (with-release [ones-vctr (entry! (vctr x (ncols x)) 1.0)]
          (if (= 1 cnt)
            ((layers 0) x ones-vctr a!)
            (with-release [temp-1 (vctr x (* max-width-1 (dim ones-vctr)))]
              (if (= 2 cnt)
                (this x ones-vctr temp-1 a!)
                (with-release [temp-2 (vctr x (* max-width-2 (dim ones-vctr)))]
                  (copy! (this x ones-vctr temp-1 temp-2) a!)))))))))
  (invoke [this x]
    (let-release [a (ge x (mrows (weights (peek layers))) (ncols x))]
      (this x a))))

The first invoke implementation is at the lowest level. It does not create any of the temporary work objects, and expects that the user provides the needed vector of ones, temp-1!, and temp-2 instances of sufficient capacity. This gives the user the opportunity to optimally manage the life-cycle of these structures. This function simply iterates through all layers, and evaluates them (recall that they are also functions) with appropriately alternated temp-1! and temp-2!.

The second invoke implementation goes one level above. It requires only input x and a matrix a!, which is going to be overwritten with the result of the evaluation. Then, depending on the number of layers, it calls the first variant of invoke in a most efficient way:

1) if the network does not have any layers, it simply copies the input.
2) if there is a single layer, it is called without initializing any temporary work memory.
3) if there are two layers, only one temporary object is needed.
4) for more than two layers, the two alternating work objects are used. The result of evaluation is copied to a! at the end.

Of course, all temporary work objects are released at the end of evaluation.

The third invoke is a pure function. It asks only for input, x, and returns the output in a new instance a. All temporary objects and mutations are encapsulated and invisible to the caller.

With these 3 variants, we have covered different trade-offs. We might pick the pure variant if we have enough resources and are concerned with code simplicity, but we can also opt for one of the destructive variants if we want, or if we have to be frugal with resources.

Since our network can automatically create temporary work objects, it needs to know their size. This is calculated during construction. The first temporary vector needs to be big enough to hold the largest output matrix in odd layers, while the second is charged with doing the same for even layers.

(defn inference-network [factory in-dim layers]
  (let [out-sizes (map #(%) layers)
        in-sizes (cons in-dim out-sizes)
        max-width-1 (apply max (take-nth 2 out-sizes))
        max-width-2 (apply max (take-nth 2 (rest out-sizes)))]
    (let-release [layers (vec (map (fn [layer-fn in-size]
                                     (layer-fn factory in-size))
                                   layers
                                   in-sizes))]
    (->NeuralNetworkInference layers max-width-1 max-width-2))))

Improving the fully-connected constructor function

The thing that might puzzle you in the implementation of inference-network is that I evaluate layers as functions. Don't they do the inference when evaluated?

In the old implementation that we have been using until now, network layers were straight functions that do the inference when evaluated. That old implementation requires the appropriate factory, input, and output dimensions, and the activation function. If we used it as-is, we would have to repeat some of these arguments, like this:

(inference-network
 factory
 [(fully-connected factory 1000 256 sigmoid)
  (fully-connected factory 256 64 tanh)
  (fully-connected factory 64 16 sigmoid)])

Some of these arguments can be supplied automatically, or inferred. If we created a mini DSL, we could supply a brief description of each layer, and the inference-network could use it to construct appropriate layer objects.

However, the DSL would take away the nice option of creating stand alone layers. This is a situation when Clojure comes to the rescue. In the following implementation, I create a closure that captures the arguments specific for each layer, while the rest of the arguments are provided when the resulting function is called, either directly, or by the neural-network constructor.

(defn fully-connected
  ([factory in-dim out-dim activ]
   (let-release [w (ge factory out-dim in-dim)
                 bias (vctr factory out-dim)]
     (->FullyConnectedInference w bias activ)))
  ([out-dim activ]
   (fn
     ([factory in-dim]
      (fully-connected factory in-dim out-dim activ))
     ([]
      out-dim))))

Here is how this API is used. Note how a call such as (fully-connected 4 tanh) is super-concise and closely resembles the domain entity it creates: a fully connected layer with 4 neurons and a tanh activation. There is no boilerplate in that call.

(with-release [x (ge native-float 2 2 [0.3 0.9 0.3 0.9])
               a (ge native-float 1 2)
               inference (inference-network
                          native-float 2
                          [(fully-connected 4 tanh)
                           (fully-connected 1 sigmoid)])
               layers (.layers ^NeuralNetworkInference inference)]
  (transfer! [0.3 0.1 0.9 0.0 0.6 2.0 3.7 1.0] (weights (layers 0)))
  (transfer! [0.7 0.2 1.1 2] (bias (layers 0)))
  (transfer! [0.75 0.15 0.22 0.33] (weights (layers 1)))
  (transfer! [0.3] (bias (layers 1)))
  (transfer (inference x a)))

nil#RealGEMatrix[float, mxn:1x2, layout:column, offset:0]
   ▥       ↓       ↓       ┓
   →       0.44    0.44
   ┗                       ┛

This appears to be working correctly with the artificial numbers we were using earlier. Zero point forty fours all the way.

Donations

If you feel that you can afford to help, and wish to donate, I even created a special Starbucks for two tier at patreon.com/draganrocks. You can do something even cooler: adopt a pet function.

The next article

I hope that the Neural Network API that I've been promising you for the last several articles is becoming material. Do you like it? Please send suggestions on how to improve it further.

There is a bit of boilerplate in how we set weights explicitly, and we will get rid of that soon. But, first, a major thing: we have to create an API for the training algorithm! We'll do that in the next article. Stay tuned for more Rock and Roll.

Thank you

Clojurists Together financially supported writing this series. Big thanks to all Clojurians who contribute, and thank you for reading and discussing this series.