Deep Learning from Scratch to GPU - 5 - Sharing Memory
February 21, 2019
Please share this post in your communities. Without your help, it will stay burried under tons of corporate-pushed, AI and blog farm generated slop, and very few people will know that this exists.
These books fund my work! Please check them out.
If you haven't yet, read my introduction to this series in Deep Learning in Clojure from Scratch to GPU - Part 0 - Why Bother?.
The previous article, Part 4, is here: Increasing Performance with Batch Processing.
To run the code, you need a Clojure project with Neanderthal () included as a dependency. If you're in a hurry, you can clone Neanderthal Hello World project.
Don't forget to read at least some introduction from Neural Networks and Deep Learning, start up the REPL from your favorite Clojure development environment, and let's continue with the tutorial.
(require '[uncomplicate.commons.core :refer [with-release let-release Releaseable release]] '[uncomplicate.neanderthal [core :refer [axpy! scal! transfer! mm! rk! view-ge mv!]] [native :refer [dv dge]] [vect-math :refer [tanh! linear-frac!]]]) (import 'clojure.lang.IFn)
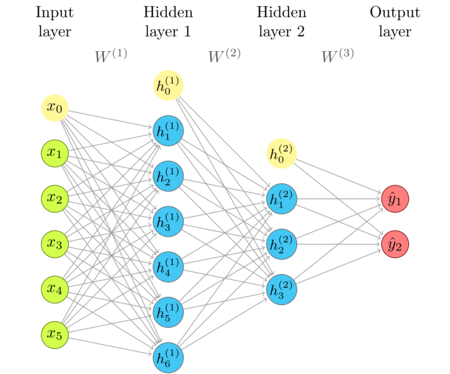
The network diagram
I'm repeating the network diagram from an earlier article as a convenient reference.
What bothers me in the current layer implementation
This is an implementation that we have from the last article.
(defprotocol Parameters (weights [this]) (bias [this])) (deftype FullyConnectedInference [w b h activ-fn] Releaseable (release [_] (release w) (release b) (release h)) Parameters (weights [this] w) (bias [this] b) IFn (invoke [_ x] (activ-fn (axpy! -1.0 b (mv! w x h)))) (invoke [_ x ones a] (activ-fn (rk! -1.0 b ones (mm! 1.0 w x 0.0 a)))))
nil#'user/fully-connected
The current structure supports both single vectors, and multiple vectors batched as columns in a matrix, as its input and output.
One thing bothers me, though: the memory that the network requires to operate. Weights and biases of each layer consume memory that is a fixed cost that we can not avoid. On the other hand, the output of each layer is relevant only during the propagation. When the signal passes to the next layer, that memory becomes irrelevant. The space it uses becomes used only when the inference is invoked with another input.
It can be argued that, when the network processes a single input, the wasted memory is not large, compared to the memory that we use for weights and bias. For example, if the input contains 200, and the output 1000 entries, the weight matrix needs 200 times more space than the output.
However, with batched input processing, the space used by the output matrix a becomes
much more relevant. In the same example of the output size of 1000, and the batch size of 1000,
the output matrix a now uses 5 times more than the weight matrix!
Let's say that the layer consists of 100,000 neurons, and we want to process 1000 inputs in a batch. The layer now uses 400 megabytes of memory for output alone. Having 10 such layers wastes 4 GB of memory, the total available on mid-range GPUs. One solution is to buy a more expensive GPU, but that does not take us far. With such relaxed approach, we soon exhaust the limits of top of the line consumer offerings, and will have to look at distributed solutions, which are much more expensive, and much slower.
Share the underlying memory
The solution is to reuse the memory. Instead of creating a new matrix for each output, we could provide one big vector, and provide submatrices of its views to each layer. The layer will not see any difference, but we would have some complication during the network setup.
(defprotocol Parameters (weights [this]) (bias [this])) (deftype FullyConnectedInference [w b activ-fn] Releaseable (release [_] (release w) (release b)) Parameters (weights [this] w) (bias [this] b) IFn (invoke [_ x ones a] (activ-fn (rk! -1.0 b ones (mm! 1.0 w x 0.0 a)))))
(defn fully-connected [activ-fn in-dim out-dim] (let-release [w (dge out-dim in-dim) bias (dv out-dim)] (->FullyConnectedInference w bias activ-fn)))
I removed the non-batch output, since it has the equivalent functionality to the batch of one.
The activation function stays the same as before.
(defn sigmoid! [x] (linear-frac! 0.5 (tanh! (scal! 0.5 x)) 0.5))
I modified the example with two layers that we used in previous articles by just replicating the same input two times. We now have two identical inputs in a testing batch of two.
Instead of creating two outputs, a-1 and a-2, I created one vector temp-a and then
took two general matrix views of that vector. view-ge creates a matrix that shares
memory with the source, but in a matrix structure. In this case, the source vector has
8 entries, which is big enough for both matrices, a \(4 \times 2\) and \(1 \times 2\) one.
(let-release [temp-a (dv 8)] (with-release [x (dge 2 2 [0.3 0.9 0.3 0.9]) ones (dv 1 1) layer-1 (fully-connected tanh! 2 4) a-1 (view-ge temp-a 4 2) layer-2 (fully-connected sigmoid! 4 1) a-2 (view-ge temp-a 1 2)] (transfer! [0.3 0.1 0.9 0.0 0.6 2.0 3.7 1.0] (weights layer-1)) (transfer! [0.7 0.2 1.1 2] (bias layer-1)) (transfer! [0.75 0.15 0.22 0.33] (weights layer-2)) (transfer! [0.3] (bias layer-2)) (layer-2 (layer-1 x ones a-1) ones a-2)))
nil#RealGEMatrix[double, mxn:1x2, layout:column, offset:0] ▥ ↓ ↓ ┓ → 0.41 0.44 ┗ ┛
The result is not as expected. Both entries should have been \(0.44\), since both inputs are the same. Where is the bug?
Be careful when sharing memory
The bug is the following. In layer-2, both the input (a-1), and the output (a-2), use
the same underlying memory buffer, the one coming from temp-a. This would not be a problem
if we weren't modifying the state of one of these matrices.
We do, however, modify a-2. The problem is that one of the inputs for this modification
is a-1. Some destructive functions support sharing input and output
(tanh! is one such function). However, most algorithms for matrix multiplication do not support sharing.
The algorithm for multiplying general dense matrices (GE) assumes that the output matrix
does not share memory with neither of the input matrices. It does not raise errors, but
the result can be corrupted.
How to know which functions do and which do not support sharing input and output memory?
Read the documentation and, when not sure, inspect the examples in numerous Neanderthal tests. Once you
get hang on the API, it is quite predictable and systematic. Most of the functions in core
do support overlap in input and output. More care should be taken for linalg functions.
So, what do we do?
In this case, the only thing that we need to take care of, is that the input and output
of the same layer do not share memory. In this case, we have only two layers, so
we get back to the same thing as before: we need two a s.
(let-release [temp-odd (dv 8) temp-even (dv 2)] (with-release [x (dge 2 2 [0.3 0.9 0.3 0.9]) ones (dv 1 1) layer-1 (fully-connected tanh! 2 4) a-1 (view-ge temp-odd 4 2) layer-2 (fully-connected sigmoid! 4 1) a-2 (view-ge temp-even 1 2)] (transfer! [0.3 0.1 0.9 0.0 0.6 2.0 3.7 1.0] (weights layer-1)) (transfer! [0.7 0.2 1.1 2] (bias layer-1)) (transfer! [0.75 0.15 0.22 0.33] (weights layer-2)) (transfer! [0.3] (bias layer-2)) (layer-2 (layer-1 x ones a-1) ones a-2)))
nil#RealGEMatrix[double, mxn:1x2, layout:column, offset:0] ▥ ↓ ↓ ┓ → 0.44 0.44 ┗ ┛
Now it's correct.
We can profit from memory reuse as we increase the number of layers, since we can alternate between these two temporary source vectors. If we only connect a few layers, that is only a hassle for no benefit, but if we need several more, and process a big batch, we can save a lot of (precious) memory.
In practice, you'll have to decide when it pays off to take this approach, but the technique, sharp as it is, is worth keeping in the toolbox. Remember its upsides, but don't forget its dangers.
The next article
The next article, CUDA and OpenCL is the one in which we finally generalize the inference layer and run it on the GPU! As you can see from the title, we'll support both major platforms, CUDA, and OpenCL, so you will be able to try this no matter what hardware you have: Nvidia, AMD, or Intel.
After that, we will finally be ready to tackle the implementation of learning.
Thank you
Clojurists Together financially supported writing this series. Big thanks to all Clojurians who contribute, and thank you for reading and discussing this series.

